Category: Ramblings

I’ve been thinking about the 23 prisoners puzzle on David Weinberger’s blog, and I’ve come up with an answer. It’s different than the one Mike Booth found. Mike’s solution has a very nice elegance to it; mine is a brute force probability solution, which relies all numbers coming up equally often–eventually.

I don’t remember enough of my statistics to calculate the expected time for my solution to free all the prisoners, but I have a strong suspicion that it’s not nearly as long as you would think. I don’t think it’s a coincidence that there are 23 prisoners in the puzzle. This is exactly the number of people you need in a room for the probability of two of them sharing a birthday to be 50% (the “Birthday Paradox”).

Anyway, here’s the (a) solution. Look away now if you want to try the puzzle on your own.

Part 1: Properties of the two-switch system

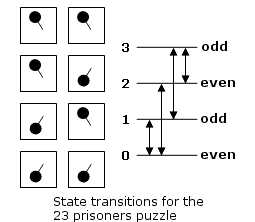
With two binary switches, you can encode four digits: 0, 1, 2, and 3. However, because you have to change the state of one and only one of the switches, there are some states the switches cannot be in when you leave the room. For example, if the switches are set to zero (off, off), you can set them to 1 (off, on) or 2 (on, off), but you can’t set them to 3, nor can you leave them at 0.

What you can always do, however, is ensure that the switches encode an odd or an even number. No matter what state the switches were in when you entered the room, it is your choice whether they end up odd or even when you leave the room. (See diagram below.) Thus, you can leave a 1-bit message to the person who enters the room the next day.

Part 2: Instructions for the prisoners

In your strategy session on the first day, every prisoner is given a number from 1 to 23. You also agree to keep a new kind of calendar, where every month has 23 days, also numbered from 1 to 23. (The names of the months are not important, just that after day 23, you roll back around to day 1 again.)

On all subsequent days, whenever you go into the switch room, you set the switches to “odd” if your prisoner number matches the number of the calendar day. If your number doesn’t match the calendar day, you sets the switches to “even”.

What you also have to do is “read” the 1-bit message the previous prisoner sent to you. As soon as you enter the switch room, you know two pieces of information:

1. The number of the previous day (e.g., day 16)
2. Whether that day’s prisoner (number 16) was in the room yesterday (if the switches were set to “odd”)

Now, all you have to do is wait, and keep track of all the days when a the correctly numbered prisoner was in the switch room the day before you. Eventually (after many months) you will have visted the switch room on all 23 days. And eventually you will reach a point where you will have marked off all the prisoner numbers on your checklist. Then you can go tell the warden to let you all go.

Will this really work?

I think so, eventually. The calculation isn’t quite the same as the Birthday Paradox, though. With birthdays, the probability of catching two on the same day increases as you get more people into the room. With the prisoner problem, even though each additional prisoner increases the chances of one of them getting an incredibly lucky streak, each additional prisoner also increases the number of “coincidence events” that are necessary for everyone to go free.

The real-world answer, of course, is that they’re all ‘gator food no matter what. Either

• A) they wouldn’t agree on a strategy on that first day, or
• B) someone would forget what strategy they’d agreed on, or
• C) the solitary confinement would drive someone mad enough to fancy their chances with the alligators instead of spending another day in the box, or
• D) the warden was just messing with their heads, and never had any intention of setting them free in the first place. He was twisted enough to come up with this scheme. Do you really think he’s going to let his evil plans be thwarted by a bunch of pesky kids?

Update: Several people have pointed out the flaw in my reasoning. I’ve written a little more about it here.

Chilli…yum. Chilli con carne, chilli chicken, deep fried shredded beef with chilli sauce. I can’t get enough of the stuff.

Peanuts…yum. Salted peanuts, shelled peanuts, peanut butter, saté sauce. I can’t get enough of the stuff.

Put them together, and you get chilli peanuts!

Which are unspeakably vile.

In terms of badness, they’re right up there with the salt and vinegar peanuts I encountered a few years ago. A mouthful of peanuts with some salt and vinegar crisps, that works just fine. But cut out the crisps, and the flavour is too much for the poor peanuts to bear on their own. Peanuts should taste of, well, peanuts. Maybe with a little salt. But dusted with mildly spicy chilli powder? No. Don’t go there.

You know the rule of thumb that says humans can only hold 7 (+ or – 2) items in short-term memory at a given time? Well, while reading Information Architecture for the World Wide Web I came across a reference to the original research on the subject.

In his opening comments, Prof. George A. Miller says:

“My problem is that I have been persecuted by an integer. For seven years this number has followed me around, has intruded in my most private data, and has assaulted me from the pages of our most public journals. This number assumes a variety of disguises, being sometimes a little larger and sometimes a little smaller than usual, but never changing so much as to be unrecognizable.”

The paper explains what the number 7 really means in terms of human perception and cognition. It’s a fascinating article, and a must-read if you enjoy knowing the true origins of such pieces of modern folk wisdom.

Further reading:

• Psychology Breakthroughs Worth Knowing: The Magical Number Seven

The last year or so has seen an almost endless stream of discussions on the subject of file sharing, peer-to-peer, music piracy, copy protection, and digital rights management. Unfortunately, most of these discussions involve only the technologists who understand the possibilities the internet brings. The publishers and money men seem to be lagging several years behind.

Napster opened in the middle of 1999. It lasted until mid 2001. That means it has been shut down for a year and a half now. And have the music publishers come up with a viable alternative? Er, no. They’ve been busy putting more extensive copy protection on their CDs so that customers (or, as they prefer, “consumers”) can’t put them up on Napster-like services in the first place.

Sigh. This is what us technologists find most frustrating. We are used to things happening in “internet time.” A new technique or standard is suggested one day, and a week later the first applications emerge. Stability is arived at in a matter of months; maturity comes within a year–two at most.

Two most interesting articles last week came from Robert X Cringely (who has been looking at these issues for the last few weeks) and Tim O’Reilly.

O’Reilly says:

“The music and film industries like to suggest that file sharing networks will destroy their industries.

Those who make this argument completely fail to understand the nature of publishing. Publishing is not a role that will be undone by any new technology, since its existence is mandated by mathematics. Millions of buyers and millions of sellers cannot find one another without one or more middlemen who, like a kind of step-down transformer, segment the market into more manageable pieces. In fact, there is usually a rich ecology of middlemen. Publishers aggregate authors for retailers. Retailers aggregate customers for publishers. Wholesalers aggregate small publishers for retailers and small retailers for publishers. Specialty distributors find ways into non-standard channels.”

Cringley says:

“The music recording industry is clinging to old habits. The world is changing, as is the way they COULD do business. Consumers are adapting, but the suppliers are not. Economics is like a seismic force. You can flow with the process or resist and cause the pressure to build. When it blows, it blows, and what could have been a process of logical evolution becomes a revolution and all the players change.”

Basically, the people who know what they’re talking about are getting sick and tired of all the heel-dragging that’s going on in the music publishing industry. (The book publishing industry is safe for a few years yet, because screen technology isn’t good enough to replace books.)

Here’s what I want out of a digital music service:

• I want to type in the name of a song–any song–and get it. This was the original power of Napster. “Peer-to-peer” was just a distraction.
• I want to be able to listen to songs on whatever device I like. If I download the song at home, I don’t want to have to pay again to listen to it at work, or on my minidisc player. Right now, the program that Sony provides with my minidisc player only allows me to place a single song on three different discs. I want to mix the music I’ve bought in any way I like.
• I also want to be able to give a copy of a CDs or a minidisc to family or friends, to show them what I’m listening to, or to introduce them to cool new bands.
• I want the digital format to be an open standard, so that–in principle–it can be played on any platform that chooses to support it. A proprietary format that only works on Windows isn’t going to cut it. Next year, I might decide to stick with Linux 🙂
• I want to pay a fixed monthly fee for this service. I don’t want to have to think–let alone worry–about how much I’m spending when I listen to music. Having to watch the clock is a pain in the butt. Flat-fee, always-on, makes using the Internet just so much more pleasant. Going back to a per-minute or per-song system would seem like too much of a backwards step.
• I want to pay for my music. I want to see the artists rewarded for their work. I want to see the publishers rewarded for their part in bringing the music to me.

Why is this so difficult? The technology to do this has been around for years.

I understand the concept of copyright, and I’m happy with it. I produce content (text, photos), and I don’t want people ripping it off. But there’s a difference between mass copying, and copying on a personal scale. One is piracy, and the other is free publicity. A system that does all the things I’ve outlined above would inhibit the former, while encouraging the latter.

I wish the music publishers would stop concentrating on copy protection, and start thinking about convenience. It’s just common sense.