Author: Martin

As both Mike Booth and my wife pointed out, my solution to the 23 Prisoners Problem is flawed. It works if the warden takes one prisoner into the switch room every day, but the puzzle explicitly says that this isn’t the case:

“After today, from time to time whenever I feel so inclined, I will select one prisoner at random and escort him to the switch room.”

Damn. I’d felt so pleased with myself for figuring it out. I even sent David Weinberger a link to my solution. He posted a link to it on his blog, which means that I can’t go back and destroy all evidence of trying…. Curse the permanence of the web!

My solution tried to solve the problem by allowing the prisoners to add some extra bits of information to the problem. But the problem is phrased very carefully to ensure that no extra information beyond the state of those two switches can be inserted. The random selection of prisoners, and the random interval between them being picked, effectively destroys any attempt to pass state information in any other way.

Mike’s solution is wonderfully elegant, but I can’t help feeling that there is another way it can be done. The fact that problem emphasises the evenness of the random distribution (“But, given enough time, everyone will eventually visit the switch room as many times as everyone else.”) makes me think that there is a probabilitistic answer somewhere. Also, with there being exactly 23 prisoners, I can’t help but wonder about a connection with the Birthday Paradox.

Or maybe the number 23 is just a coincidence stemming from the Law of Small Numbers (i.e., there aren’t enough small numbers for each of them to have a unique purpose).

More pondering is required.

I’ve been thinking about the 23 prisoners puzzle on David Weinberger’s blog, and I’ve come up with an answer. It’s different than the one Mike Booth found. Mike’s solution has a very nice elegance to it; mine is a brute force probability solution, which relies all numbers coming up equally often–eventually.

I don’t remember enough of my statistics to calculate the expected time for my solution to free all the prisoners, but I have a strong suspicion that it’s not nearly as long as you would think. I don’t think it’s a coincidence that there are 23 prisoners in the puzzle. This is exactly the number of people you need in a room for the probability of two of them sharing a birthday to be 50% (the “Birthday Paradox”).

Anyway, here’s the (a) solution. Look away now if you want to try the puzzle on your own.

Part 1: Properties of the two-switch system

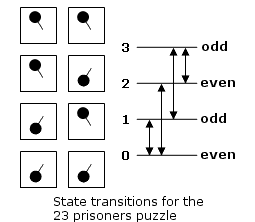
With two binary switches, you can encode four digits: 0, 1, 2, and 3. However, because you have to change the state of one and only one of the switches, there are some states the switches cannot be in when you leave the room. For example, if the switches are set to zero (off, off), you can set them to 1 (off, on) or 2 (on, off), but you can’t set them to 3, nor can you leave them at 0.

What you can always do, however, is ensure that the switches encode an odd or an even number. No matter what state the switches were in when you entered the room, it is your choice whether they end up odd or even when you leave the room. (See diagram below.) Thus, you can leave a 1-bit message to the person who enters the room the next day.

Part 2: Instructions for the prisoners

In your strategy session on the first day, every prisoner is given a number from 1 to 23. You also agree to keep a new kind of calendar, where every month has 23 days, also numbered from 1 to 23. (The names of the months are not important, just that after day 23, you roll back around to day 1 again.)

On all subsequent days, whenever you go into the switch room, you set the switches to “odd” if your prisoner number matches the number of the calendar day. If your number doesn’t match the calendar day, you sets the switches to “even”.

What you also have to do is “read” the 1-bit message the previous prisoner sent to you. As soon as you enter the switch room, you know two pieces of information:

1. The number of the previous day (e.g., day 16)
2. Whether that day’s prisoner (number 16) was in the room yesterday (if the switches were set to “odd”)

Now, all you have to do is wait, and keep track of all the days when a the correctly numbered prisoner was in the switch room the day before you. Eventually (after many months) you will have visted the switch room on all 23 days. And eventually you will reach a point where you will have marked off all the prisoner numbers on your checklist. Then you can go tell the warden to let you all go.

Will this really work?

I think so, eventually. The calculation isn’t quite the same as the Birthday Paradox, though. With birthdays, the probability of catching two on the same day increases as you get more people into the room. With the prisoner problem, even though each additional prisoner increases the chances of one of them getting an incredibly lucky streak, each additional prisoner also increases the number of “coincidence events” that are necessary for everyone to go free.

The real-world answer, of course, is that they’re all ‘gator food no matter what. Either

• A) they wouldn’t agree on a strategy on that first day, or
• B) someone would forget what strategy they’d agreed on, or
• C) the solitary confinement would drive someone mad enough to fancy their chances with the alligators instead of spending another day in the box, or
• D) the warden was just messing with their heads, and never had any intention of setting them free in the first place. He was twisted enough to come up with this scheme. Do you really think he’s going to let his evil plans be thwarted by a bunch of pesky kids?

Update: Several people have pointed out the flaw in my reasoning. I’ve written a little more about it here.